Bu yazı derin öğrenme ile ilgili yazı serimizin dördüncü başlığıdır. Konular birbirinin devamı niteliğinde olup önceki yazılara referanslar içermektedir. Bu nedenle baştan başlayarak sırayla okumalısınız. Önceki yazılarımız:
- Derin Öğrenmeye Genel Bakış
- Derin Öğrenmeye Genel Bakış – 2
- Derin Öğrenme – 28 Kod Satırı ile Çalışan Bir Beyin Yapmak
İlk üç yazıyı okumuşsanız devam etmeye hazırsınız. Haydi başlayalım.
57-59. Satırlar
Bu ağımızın tahminde bulunduğu kısımdır. Derin öğrenme sürecinin heyecan verici bir kısmı olduğu için aynı kavramı üç farklı prespektiften ele alacağız:
1 – İlk önce ileri beslemeyi masalsı bir dille anlatacağız,
2 – İkinci olarak ileri beslemenin harika çizimlerini göreceğiz ve
3 – Motor kapağını açarak ileri beslemenin motoru matriks çarpımını çalışacağız.
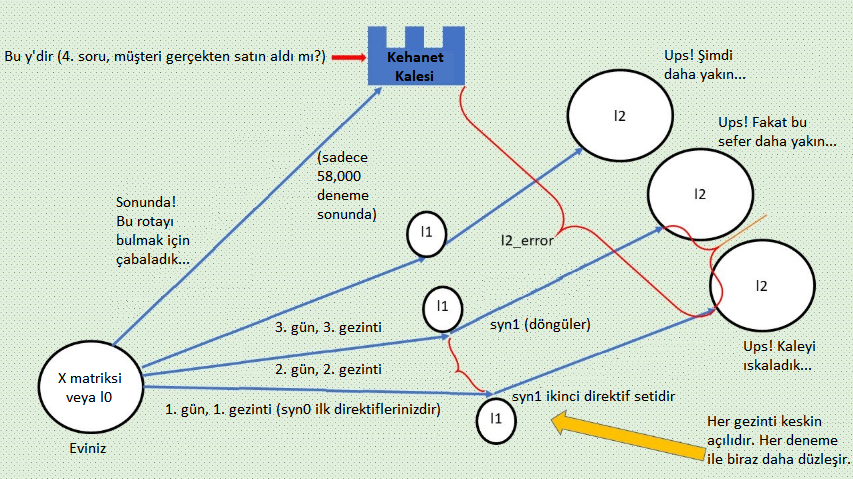
Kale ve Hayatın Anlamı: İleri Besleme Ağı
Kendinizi bir nöral ağ olarak hayal edin. Geçerli bir ehliyeti olan, hızlı arabalardan ve mistik ruhani yolculuklardan hoşlanan bir nöral ağsınız. Hayatın anlamını bulmak için sabırsızlanıyorsunuz. Şu işe bakın ki mucizeler içinde bir mucize gerçekleşiyor ve belli bir kaleye giderseniz mistik kahininizin hayatın anlamını açıklamak için sizi beklediğini öğreniyorsunuz. Sevinç içindesiniz!
Söylememize bile gerek yok, Kahinin kalesini bulmak için oldukça motivesiniz. Sonuçta kahin gerçeği (gerçek gerçeği) temsil ediyor, yani mistik sorumuz “Kedim Mis! satın aldınız mı?”nın cevabını. Ne kadar da gizemli! (Başka bir deyişle eğer tahmininiz kahinin gerçeği ile eşleşirse kalede olursunuz, önceki yazılarımızdan bildiğiniz l2 hatasının sıfır olduğu, sarı okun sıfır yükseklikte olduğu, beyaz topun kasenin tabanına ulaştığı yerde. Bunların hepsi aynı şeydir.)
Ne yazık ki kahinin kalesini bulmak biraz sabır ve devamlılık gerektirir. Çünkü kaleye ulaşmayı binlerce kere denediniz ve kayboldunuz.
(İpucu: Binlerce gezinti = denemeler. “Kaybolmak” l2 öngörünüzde hala hata olduğu anlamına gelir. Bu da sizi gerçeğin kalesi y’den uzakta tutar. Burada fazla basite indirgediğimizi hatırlatayım. Pratikte kahine ulaşacağınızın bir garantisi yoktur. Sadece lokal minimuma gidiyor olduğunuzu bilebilirsiniz ve bu da sadece fonksiyonunuz konveks ise mümkündür. Tipik olarak hata yukarı ve aşağı gider ancak burada eğitim amacıyla basitleştirilmiş masalsı örneğimize sadık kalacağız. Sonuçta hepimiz mutlu sonları seviyoruz.)
Fakat harika haberler var: Biliyorsunuz ki her gün, her gezintinizle beraber kahine gittikçe daha çok yaklaşıyorsunuz (y vektörü tüm sevimliliği ile… baş döndürücü). Kötü haber ise kaleye ulaşamadığınız her seferinde, PUFF! ertesi sabah tekrar evinizde uyanıyorsunuz (yani Tabaka 0’da, l0 veya 3 anket sorumuzun cevaplarından oluşan girdi özelliklerinde). Buradan tekrar başlamanız gerekiyor (yeni bir deneme). Bu biraz şuna benziyor:
Neyse ki bu hikayenin mutlu bir sonu var. Ancak kahinin kalesine ulaşmak ve aydınlanma yaşamak için belki de 58,000 deneme daha yapıp rotanızı düzeltmeniz gerekiyor. Endişelenmeyin, buna değecek.
Şimdi eviniz X’den kale y’ye olan gezintilerden birine bakalım. Yaptığınız her gezinti 57-59. satırlardan geçen bir ileri beslemedir. Her gün yeni bir yere sadece orasının kale olmadığını keşfetmek için varıyorsunuz. Hay aksi! Elbette bir sonraki sefere gurunuza nasıl biraz daha yaklaşabileceğinizi bulmak istiyorsunuz. Bunu aşağıdaki adımlarda göreceğiz. Kahin ve Kale, Hatalarınızdan Öğrenmek için benimle kalın.
Tamam, yukarıdaki kahin kalesi benzetmesi ileri besleme süreci için bir benzetmeydi. Bundan sonra ileri beslemenin basitleştirilmiş bir örneği üzerinden gideceğiz.
İleri Beslemenin Baş Döndürücü Güzellikte Şemaları
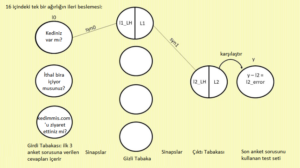
16’sı içinde sadece bir ağırlık örneğini ele alacağız. Çalışacağımız ağırlık syn0’ın 12 sırasının en üstü, tepedeki l0 ve l1 nöronları arasında olacak. Basitlik adına buna syn0,1 diyelim (teknik olarak “matriks syn0’ın 1. satır, 1 sütunu” için doğru isimlendirme syn0(1,1)’dir.). Nasıl göründüğüne bakalım:
Neden l2 ve l1 nöronlarını temsil eden daireler ortadan ikiye bölündü? Dairenin sol yarısı (l’nin kullandığı değişkenler “LH” ile gösterildi) sigmoid fonksiyonda girdi olarak kullanılan değerdir ve sağ taraf ise sigmoid fonksiyonun çıktısıdır: l1 veya l2. Bu bağlamda, sigmoidin önceki tabakadaki ürünü alıp 0 ile 1 arasındaki bir değere sıkıştırdığını hatırlayın. Bu kodun şu parçasıdır (10. satırda oluşturulmuştur ancak 58. satıra kadar çağırılmaz):
return 1/(1+np.exp(-x))
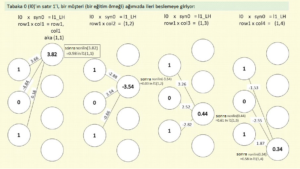
Tamam, işte ileri besleme alıştırma örneklerimizden birini kullanıyor, l0’ın ilk satırı veya “birinci müşterinin 3 anket sorusuna olan cevabı”: [1,0,1]. Böylece l0’ın ilk değerini syn0’ın ilk değeri ile çarpmaya başlarız. syn0 matriksimizin onu başlattığımızdan beri (önceki yazımızın Rastgele Sayılar Yerleştirmek bölümü) bazı eğitim denemelerinden geçtiğini hayal edin. Şimdi şuna benziyor:
syn0:
[ 3.66 -2.88 3.26 -1.53]
[-4.84 3.54 2.52 -2.55]
[ 0.16 -0.66 -2.82 1.87]
Şimdi şöyle düşünebilirsiniz, “Neden syn0’ın değerleri bir önceki yazıda oluşturduğumuz syn0’dan bu kadar farklı?” Sormanıza sevindim. Önceki matrikslerin çoğu bilgisayarda henüz üretilmiş rastgele sayılarmış gibi gerçekçi başlangıç değerleridir. Fakat burada ve daha aşağıdaki matriksler başlangıç değerleri değildir. Bunlar bazı eğitim denemelerinden geçmiş matrikslerdir. Değerleri öğrenme sürecinde güncellenerek oldukça değişmiştir.
Güzel. Haydi l0’ın “1”’ini syn0’ın “3,66”sı ile çarpalım ve bu saçmalığın bizi nereye götürdüğüne bakalım:
Burada yalancı-kodda ileri beslemenin neye benzediğini görüyoruz. Yukarıdaki şemada ileri, soldan sağa olan süreci takip edebilirsiniz. (Bu şemada “LH” sol anlamında eklenmiştir. Böylece dairenin sol yarısını, verilen tabakadaki bir nöronu göstermede kullanıyoruz. “l1LH”nın anlamı “l1’i temsil eden dairenin sol yarısı”dır. Bu da “ürün nonlin() fonksiyonunu geçmeden önce” demektir.)
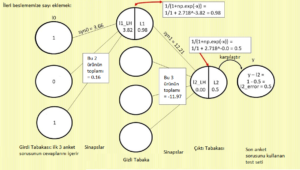
l1_LH = l0 x syn0 so l1_LH = 1 x 3.66 -> (Ardından diğer l0 değerleri x diğer syn0 değerleri’nin ürünlerini eklemeyi unutmayın. Şimdilik basitlik adına bunların toplam 0.16 ettiği konusunda bana güvenin) -> l1_LH = 1 x 3.66 + 0.16 = 3.82
l1 = nonlin(l1_LH) = nonlin(3.82) -> nonlin() = 1/(1+np.exp(-x)) = [1/(1+2.718^-3.82))] = 0.98
l2_LH = nonlin(l1_LH) = l1 -> l1 x syn1 = 0.98 x 12.21 = 11.97 (tekrar, diğer syn1 çarpımlarının sonuçlarını ekleyin–bana güvenin, bunların toplamı -11.97) -> 11.97 + -11.97 = 0.00
nonlin(l2_LH) -> nonlin() = 1/(1+np.exp(-x)) = [1/(1+2.718^0.00))] = 0.5
l2 = 0.5 -> l2_error = y-l2 -> 1 – 0.5 = 0.5 -> l2_error = 0.5
Tamam o zaman. Yukarıdaki kodu yapan matematiğin temelini aşağıda bulabilirsiniz:
Haydi İleri Beslemenin Matematiğine Yavaşça Geçelim
l0 x syn0 = l1LH, böylece örneğimizde 1 x 3,66 = 3.66, fakat l0’ın diğer iki ürünü x syn0’ın karşılık gelen ağırlıklarını eklemeyi unutmayın. Örneğimizde l0,2 x syn0,2= 0 x bir şey = 0, yani fark etmiyor. Fakat l0,3 x syn0,3 fark ediyor, çünkü l0,3=1 ve geçen bölümdeki matriks örneğinden biliyoruz ki syn0,3 değeri 0.16. Böylece l0,3 x syn0,3 = 1 x 0.16 = 0.16. l0,1 x syn 0,1 ürünümüz + l0,3 x syn0,3 ürünümüz = 3.66 + 0.16 = 3.82 ve 3.82 l1_LH’dır. Bundan sonra l1_LH’yı nonlin() fonksiyonumuzda çalıştırarak 0 ile 1 arasında bir olasılık elde etmeliyiz. Nonlin(l1_LH), return 1/(1+np.exp(-x)) kodunu kullanır. Örneğimizde bu şöyle olur: 1/(1+2.718^-3.82))=0.98, yani l1 (l1 düğümünün sağ tarafı) 0.98’dir.
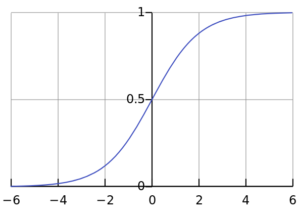
Yukarıda 1/(1+np.exp(-x)) = [1/(1+2.718^-3.82))] = 0.98 denkleminde ne oldu? Bilgisayar süslü bir kod, return 1/(1+np.exp(-x)) kullanarak gözlerimizle yapabileceğimiz bir şeyi yaptı. Aşağıdaki şekilde x = 3.82 için sigmoid eğride karşılık gelen y değerini söyledi:
X ekseninde 3.82 noktası için mavi eğride karşılık gelen y değerinin yaklaşık 0.98 olduğuna dikkat edin. Kodumuz 3.82’yi 0 ile 1 arasında bir istatistiksel olasılığa çevirdi. Bunu grafikle görselleştirmek yararlıdır, böylece anlaşılmaz bir hokus pokus olmadığını anlayabilirsiniz. Bilgisayar da bizim yaptığımızı yapar: X eksenindeki 3.82’nin y ekseninde neye karşılık geldiğini bulmak için gözlerini değil de matematiği kullanır, daha fazlası değil.
Tekrarlayalım: nonlin() sigmoid fonksiyonun herhangi bir sayıyı 0-1 arasındaki değere dönüştüren kısmıdır. Bu return 1/(1+np.exp(-x)) kodudur. Bu eğim almaz. Fakat geri yayılmada sigmoid fonksiyonun diğer parçasını, eğim alan kısmını kullanacağız, örneğin return x*(1-x) . Çünkü 57 ve 71. satırlar spesifik olarak sigmoidin kod ile eğimi almasını ister (deriv==True) .
Şimdi durup bir daha tekrar edelim. l1 değerimizi syn1,1 değerimiz ile çarpıyoruz. l1 x syn1 = l2LH bizim örneğimizde 0.98 x 12.21 = 11.97. Ancak unutmayın ki 11.97’ye diğer tüm l1 nöronlarının ürünler kere onlara karşılık gelen syn1 ağırlıklarını eklemeliyiz. Basitlik adına bana güvenin, sonuçta -11.97 oluyor (aynı matriksi kullanarak). Sonuçta 11.97 + -11.97 = 0.00 oluyor l2_LH. Daha sonra l2_LH’i harika nonlin() fonksiyonumuzda çalıştırıyoruz. Bu da şöyle oluyor: 1/(1+2.718^-(0)) = 0.5, işte gerçeği temsil eden y için ilk tahminimi l2’yi elde ettik! Tebrikler! İlk ileri beslemenizi tamamladınız!
Şimdi açıklık için tüm değişkenlerimizi tek yerde birleştirelim:
l0=1
syn0,1=3.66
l1_0.98
syn1,1=12.21
l2_LH=0
l2=~0.5
y=1 (Bu anketin dördüncü sorusu “Kedim Mis! aldınız mı?” ya verilen cevaptır.
l2_error = y-l2 = 1-0.5 = 0.5
Tamam, şimdi tüm bunları meydana getiren matriks çarpımına bakalım.
İlk önce, 58. satırda 4×4’lük bir matriks olan (gizli tabaka) l1’i oluşturmak için 4×3 l0 ile 3×4 syn0’ı çarptık:
Şimdi onu 58. satırdaki “nonlin()” fonksiyonundan geçiriyoruz, bu yukarıda açıkladığımız gibi tüm değerleri 0 ile 1 arasına sıkıştıran süslü bir matematiksel ifadedir:
1/(1 + 2.781281^-x)
Bu ağımızın gizli tabakası olan l1’i oluşturur:
l1:
[0.98 0.03 0.61 0.58]
[0.01 0.95 0.43 0.34]
[0.54 0.34 0.06 0.87]
[0.27 0.50 0.95 0.10]
Eğer matriks çarpımının görüntüsünden korktuysanız, korkmayın. Basitten başlayıp çarpımımızı küçük kısımlara ayıracağız. Böylece nasıl olduğunu anlayabileceksiniz. Girdimizden tek bir basit örnek alalım. Satır 1 (birinci müşterinin anket cevapları): [1,0,1] bir 1×3’lük matrikstir. Bunu syn0 ile yani 3×4’lük matriksle çarpacağız ve yeni l1’imiz 1×4’lük bir matriks olacaktır. Bu işlem şu şekilde görselleştirilebilir:
(l0’ın satır 1’ini syn0’ın sütun 1’i ile çarpın, ardından satır 1’i sütun 2 ile çarpın vb)
l0’ın satır 1’i: syn0’ın sütün 1’i:
[1 0 1] x [ 3.66] + [ 3.82 -3.54 0.44 0.34]
[1 0 1] x [-4.84] + = [ (l0’ın satır 2’si x syn0’ın sütün 1, 2, 3 ve 4’ü…) ]
[1 0 1] x [ 0.16] [ vb… ]
Ardından yukarıdaki 4×4’lük sonucu “nonlin()”’den geçirerek l1 değerlerini elde edin.
l1:
[0.98 0.03 0.61 0.58]
[0.01 0.95 0.43 0.34]
[0.54 0.34 0.06 0.87]
[0.27 0.50 0.95 0.10]
Satır 58’de l1’in sigmoid fonksiyonunu aldığımıza, çünkü l1’in 0 ve 1 arasında bir değer alması gerektiğine dikkat edin:
l1=nonlin(np.dot(l0,syn0))
Satır 58’de sigmoid fonksiyonun dört büyük avantajından ilkini görüyoruz. l0 matriksi ile syn0 çarpımının sonucunu nonlin() fonksiyonundan geçirdiğimizde sigmoid, matriksteki her değeri 0 ve 1 arasında bir istatistiksel olasılığa dönüştürüyor.
Şimdi neyin istatistiksel olasılığı diye sorabilirsiniz. O halde kendinizi derin öğrenmedeki bir sonraki harikaya hazırlayın.
Süper Anahtar Nokta: Gizli Tabakanın Çıkarım Korelasyonları
Ah evet, doğru, istatistiksel olasılıklar. İyi de neden umursayalım? Çünkü istatistiksel olasılık bir grup aptal matriksin aniden canlanması ve bir çocuk beyni gibi öğrenmeye başlamasının ana etkenlerindendir. Bunun dışında ilginizi çekmesi için hiçbir neden yok…
Birinci tabakada l0’ı syn0 ile çarptığımızda neden syn0’daki ağırlıkların farklı değerleri ile vakit kaybediyoruz? Çünkü orijinal üç sorumuzun çeşitli kombinasyonlarını deneyerek hangi kombinasyonun esas merakımız olan “Müşterinin Kedim Mis! satın alma ihtimali nedir?”i öngörmemize en fazla yardım edeceğini görmek istiyoruz. Birkaç aptalca örnek üzerinden devam edelim:
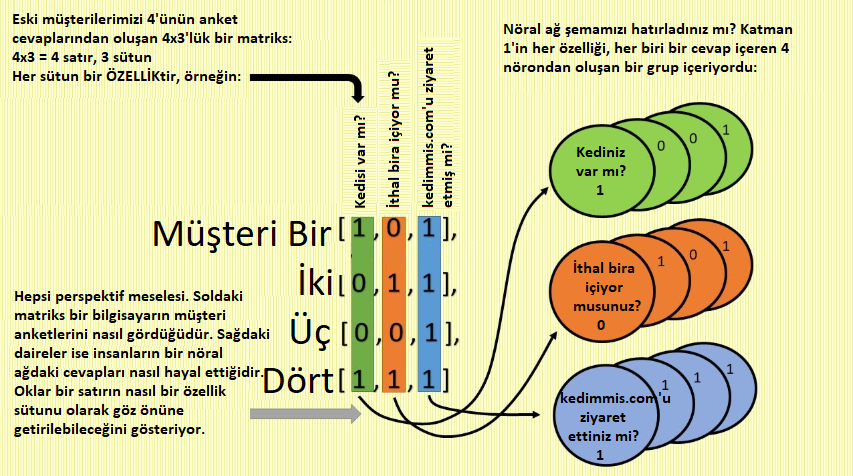
Orijinal üç anket sorumuza olan müşteri cevaplarına sahibiz. Bu soruların farklı kombinasyonlarından tahmin becerimizi arttıracak ne gibi sonuçlar çıkarabiliriz? Örneğin eğer müşterinin kedisi varsa bu evcil hayvan zevkinin harika olduğunu gösterir. Eğer ithal bira içiyorsa bira zevkini önemsediğini gösterir. Böylece bu müşterilerin Kedim Mis!’in harika, zevkle tasarlanmış koku emici granüllerini sadece döşemelerinde gururla sergilemek için bile alacağı sonucunu çıkarabiliriz, kedileri kakalarını sadece dışarıya yapıyor olsa bile! Bu nedenle eğer bize daha doğru tahminler sağlıyorsa bu iki özellik arasındaki bağı kuvvetlendirebiliriz.
Başka bir örnek: Eğer müşterinin bir kedisi yoksa ancak ithal bira içiyor ve kedimmis.com’u ziyaret etmişse teknolojiden anladıkları sonucunu çıkarabiliriz. İthal bira içmelerinin sebebi açıktır ki sadece Hollandalı bir markanın oradan evlerine ulaşması sağlayan lojistik zincirini takdir ettikleri içindir. Üstelik bir de internet sitelerini ziyaret ediyorlar ve diğer her şey… Yaa… Bu insanlar teknoloji delisi dahiler olmalı. O halde teknolojik olarak sofistike müşterilerin Kedim Mis!’i sadece her kaka emicinin yapısındaki en yeni teknolojiye hayran oldukları için alacağı sonucunu çıkarabiliriz. Müşterinin bir kedisi olmamasına rağmen. Belki de syn0’daki ağırlıkları bu ince özellikler arasındaki bağları kuvvetlendirecek şekilde değiştirmeli ve daha doğru tahminlerin keyfini çıkarmalıyız.
Anladınız mı? l0’daki anket sorularına cevaplar ile syn0’daki ağırlıkları çarptığımızda (her ağırlık bir çıkarım korelasyonunun öngörümüzde ne kadar önemli olduğuna dair en iyi tahminimizdir) anket cevaplarımızın farklı kombinasyonlarını deneyerek hangisinin kimin Kedim Mis! alacağını öngörmede en yararlı olduğunu bulmaya çalışıyoruz. 60,000 deneme sonunda açıkça ortaya çıkıyor ki, örneğin kedimmis.com’u ziyaret edenler Kedim Mis! almaya en yatkındır ve buna karşılık gelen ağırlıklar denemeler boyunca artar. Bu da istatistiksel olasılığın 1’e 0’dan daha yakın olduğu anlamına gelir. Ancak kedisi olmayan ithal bira içiciler Kedim Mis! almaya daha az yatkındır. Bu nedenle ağırlıkları azalır, yani istatistiksel olasılıkları 0’a 1’den daha yakın olur. Havalı, değil mi? Sayılarla bir şiir gibi. Mantığı olan ve düşünen matriksler!
İşte bunun bu kadar önemli olmasının nedeni. Motor kapağının altında “Pandora’nın Kutusu” veya “Gizemli bir sihir” yok. Açık, zarif ve güzel matematik var. Ve bunda ustalaşabilirsiniz. Sabır ve devamlılık gerektirir sadece.
Sakinleşin ve matriksleri çarpmaya devam edin.
Matriks Çarpımını Nöron ve Sinapslarla Görselleştirmek
Bu l0 ve syn0 değerlerini nöron ve sinapslardan oluşan benzetmemize yerleştirirsek şöyle görünür:
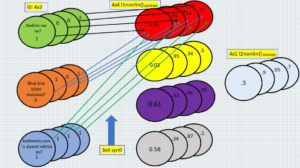
Yukarıdaki şekil l0’daki birinci satır girdilerinin ağımızı beslemesinin ilk adımını gösteriyor. Birinci satırın birinci müşteri ve üç anket sorusuna verdiği üç cevap olduğunu biliyorsunuz. Ama sıra bu sayıları syn0’ın tüm 12 değeri ile çarpmaya ve aynısını diğer üç müşterinin üç değeri ile yapmaya geldiğinde, tüm bu sayılarla nasıl başa çıkıp düzenleyeceğiz?
Burada anahtar nokta dört müşterinin “grup” halinde bir arada olduğunu düşünmektir. Yani en üst sıradaki en üst grup birinci müşteridir. Yukarıda gördüğünüz gibi, satır birin üç sayısını syn0’ın 12 sayısının tamamıyla çarparız, toplarız ve l1’in üst grubundaki dört değeri elde ederiz.
Gruptaki ikinci paket nedir? İkinci müşterinin ikinci soruya olan cevaplarından oluşan 0,1,1 şeklindeki ikinci sıra, ikinci pakettir. Bu üç sayıyı syn0 değerlerinin 12’si ile çarpıp toplayarak l1 değerleri grubunun ikinci paketindeki dört değeri elde ederiz.
Böyle iki defa daha devam eder. Anahtar nokta her seferinde bir paketten öğe almaktır. Böyle olunca grubunuzda dört paket de olsa, dört milyon paket de olsa fark etmez. Her özelliğin kendi değer grubu olduğunu, bizim örneğimizde her anket sorusunun (özelliğin) dört müşterimizden gelen dört cevaptan oluşan bir grubu olduğunu söyleyebilirsiniz. Fakat bu dört milyon da olabilirdi. Bu “tam grup kombinasyonu” kavramı oldukça yaygın bir modeldir. Bu nedenle açıklamaya çalıştım. Verilen bir özelliğin kendi değer grubu olduğunu düşünmek anlamayı kolaylaştırabilir. Bir özellik gördüğünüzde artık onun altında bir değer grubu olduğunu bilirsiniz.
Satır 59’da 4×4 l1 ve 4×1 syn1’in nokta sonucunu alırken tam olarak aynı şey olur, ardından bu sonucu sigmoid fonksiyonda çalıştırarak her değerin 0-1 aralığında bir istatistiksel olasılık olduğu 4×1 l2’yi meydana getiririz.
l1 (4×4)
[0.98 0.03 0.61 0.58] [12.21]
[0.01 0.95 0.43 0.34] x [10.24] =
[0.54 0.34 0.06 0.87] [ -6.31]
[0.27 0.50 0.95 0.10] [-14.52]
Ardından yukarıdaki 4×1 sonucunu “nonlin()”den geçirerek tahminimiz olan l2’yi elde ederiz:
l2:
[ 0.50]
[ 0.90]
[ 0.05]
[ 0.70]
Peki bu dört tahmin bize üstün kedi temizlik ürünümüz hakkında ne söylüyor? Söylediği şey, değer 1’e yaklaştıkça müşterinin Kedim Mis! almasının daha kesin olduğudur. Değer 0’a yaklaştıkça ise Kedim Mis! almaması daha kesindir. 0.2 “Muhtemelen almayacak” demekken 0.8 “Muhtemelen alacak” demektir ve 0.999 “Kesinlikle alacak!” gibi yorumlanabilir.
Ağımızın ileri besleme kısmını tamamlamış olduk. Umarım şimdiye kadar yaptığımız şeyleri görselleştirebilmişsinizdir. Bunlar:
1 – Kullanılan matriksler;
2 – Müşteri olarak sıra dizileri;
3 – Özellikler olarak sütunlar ve
4 – Her özelliğin değer grupları içermesi (örneğin anket sorularına cevaplar);
Eğer bu dört öğeyi gözünüzün önüne getirebiliyorsanız tebrikler.
Yukarıdaki ileri beslemeyi ilk tahminimiz olarak düşünün. Bunun ardından 60,000 daha gelecek. Sonraki adımımız ilk tahminimizin nerede yanlış olduğunu hesaplamak ve ağımızın ağırlıklarını nasıl değiştireceğimizi bularak sonraki tahminimizin daha iyi olmasını sağlamaktır. Aynı tahmin etme ve iyileştirme sürecini tekrar tekrar yapacağız. 60,000 kere. Bu deneme-yanılma ile öğrenmedir ve iyi bir şeydir.